
Tous les amateurs de tennis ont déjà entendu parler de l’importance du 7e jeu dans un set en cas d’égalité (3-3). En France, cette idée a été popularisée notamment par Jean-Paul Loth, qui a commenté Roland-Garros pour France TV pendant de nombreuses années. Celui-ci confiait à Slate en 2011 :
C’est Henri [Cochet] qui s’était livré à une petite enquête sur ce sujet et s’était aperçu qu’à 3-3 survenaient souvent les breaks à cause d’une chute dans la concentration des joueurs.
L’Equipe a publié en 2016 un article qui débunke ce mythe tennistique, en relatant des analyses statistiques (assez complexes) du spécialiste Jeff Sackmann. Pour ma part, j’ai fact-checké cette idée en réalisant des analyses beaucoup plus simples qui consistent à quantifier l’effet d’un break à différents stades d’un set. Si la théorie du 7e jeu est vraie, alors un break à 3-3 devrait avoir un impact plus important sur l’issue du set qu’un break à 0-0, 1-1, 2-2 ou 4-4.
Les données analysées sont celles du tournoi simple messieurs de l’Open d’Australie 2025 (il manque juste les demi-finales et finales). Merci à Foucauld Henin pour ces données ! Ce dataset comporte le détail de chaque point joué. En retirant les quelques sets où l’un des joueurs a abandonné, on dispose de 463 sets complets.
Le tableau ci-dessous montre la probabilité de gagner le set en fonction de l’issue d’un jeu : le 1er jeu, le 3e jeu, le 5e jeu, le 7e jeu, et le 9e jeu (je n’ai pas analysé le 11e jeu car cette situation est plus rare, il faudrait un dataset plus conséquent).
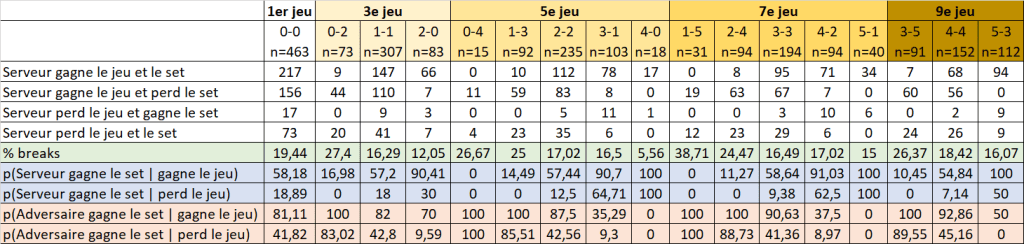
Plusieurs résultats intéressants apparaissent :
1) Le pourcentage de breaks dans ces jeux est aux alentours de 20 %. Par exemple, il y a 19,44 % de breaks dans le 1er jeu. Ce résultat est cohérent avec l’intuition que chez les hommes, il est difficile de breaker, en particulier sur surface rapide comme à l’Open d’Australie. Et on constate par ailleurs que les breaks ne sont pas plus fréquents à 3-3 (16,49 %), ce qui contredit l’affirmation d’Henri Cochet.
2) L’effet d’un break est important en général, c’est-à-dire quel que soit le jeu et le score. Par exemple, dans le 3e jeu à 2-0, le serveur a 90,41 % de chances de gagner le set s’il conserve son service contre 30 % s’il le perd.
3) L’effet d’un break dans le 7e jeu à 3-3 est important : le serveur a 58,64 % de chances de gagner le set s’il conserve son service contre 9,38 % s’il le perd. On pourrait penser que cela conforte la théorie du 7e jeu : si le serveur perd son service à 3-3, le set est quasiment plié. Mais on constate que l’effet d’un break à 3-3 est globalement identique dans les autres cas d’égalité (à 0-0, 1-1, 2-2 ou 4-4). A 0-0 par exemple, le serveur a 58,18 % de chances de gagner le set s’il conserve son service contre 18,89 % s’il le perd.
En résumé, la perte de son service dans le 7e jeu à 3-3 a un effet massif sur l’issue du set. Mais cet effet n’est pas spécifique au 7e jeu : on observe la même chose dans les autres jeux à égalité. Reste à voir si ce résultat se vérifie a) sur d’autres surfaces, et b) chez les femmes, la surface et le genre étant des facteurs pouvant influencer les dynamiques de break.